There are two distinct methods of travelling between worlds. Hyperdrive uses the Mental Power of a psionic navigator to travel instantaneously from star system to star system. Unfortunately, hyperdrive will not work when a spaceship is within the gravity well of a star system. Thus, slower-than-light reaction drive (fission) is used to travel from planet to planet within a star system. A character conducting a hyperjump uses his navigator skill (this skill is not used to navigate a spaceship through interplanetary space). Pilot skill is used to control a spaceship through interplanetary space.
All the spaceships in Universe are composed of a hull and a variable number of pods. The hull determines the ship's size and overall performance. The pods are attached to the hull and give the ship a specific character: military, scientific, merchant, passenger, etc. This concept is more fully explained in Delta Vee Sections 1.0 through 5.0.
The Gamesmaster creates spaceships from the various hulls and pods and introduces them into play so that the characters may travel in them, encounter them and, if wealthy enough, purchase them.
Two astronomical terms are used in this Chapter:
Astronomical Unit (AU). A standard measure of distance in interplanetary space. One AU equals 149 million km, the distance from Sol to Earth.
Ecliptic. The plane formed by a star and the orbital paths of all the planets around it. The mass of the worlds scattered around the ecliptic create a flattened sphere of gravity wells that may not be entered when hyper-jumping.
Spaceship hulls and pods are manufactured on worlds with Class 3 and 4 spaceports, and in orbiting factories attached to such spaceports. Like all other manufactured goods, spaceship parts come in a variety of Civ Levels (6,7,8) and will only be readily available on a world of an equal or higher Civ Level. Spaceships are far beyond the financial means of most people and, thus, the characters will be little concerned with the economics of spaceship construction and purchase. However, the characters will be able to book passage in commercial spaceships and during an adventure will sometimes receive free transport by an employer or may even be loaned a ship for the completion of a specific mission.
The GM uses the list of hulls and pods in this Section and the additional information in the Delta Vee rules (especially concerning military spaceships) to create spaceships suited to his adventures. The hull/pod system allows the GM to design a wide variety of ships with a minimum of trouble. When constructing a ship, the GM should keep in mind the specifications of each hull and pod, especially their availability. Civ Level, and crew requirements, so that, when assembled, the ship may be logically (and legally) used by the characters.
Each hull possesses a sub-light engine (using radioactives as its energy source, see 33.2), a bridge with basic navigation and communications equipment, living quarters and first aid station for a crew necessary to keep the craft running, an airlock leading out of the ship, and a docking port for rendezvous with other craft, and all the attributes listed in Delta Vee 4.0 (especially Table 4.9, the Spaceship Attribute Chart).
Four industrial concerns produce the spaceships:
Terwillicker Spaceworks, Inc. manufactures the Terwillicker-5000, a high-quality two-person craft; and the Terwillicker-X fighter, an innovative adaptation of the 5000 designed for military use.
Blades Research Institute produces military craft under long-term contract. The Dagger, Sword, and Spear Class ships are their most successful models.
Harmonics, Inc. specializes in finely crafted ships for government and high-level corporate use. The Piccolo, Flute, and Clarinet represent the top of their line.
The Corco Group manufactures a large line of commercial vessels, often sacrificing performance for economy. The Gamma, Zeta, and Mu Classes are well suited for transport in safe regions. The Iota is designed to appeal to merchants working in dangerous areas.
Additional information is listed with each spaceship hull description in 31.2. This information includes the following:
Availability (Open, Restricted, or Closed). An open spaceship is available for purchase by anyone who has the funds. A restricted spaceship is available only with permission from the federation or an independent world. Such ships, equipped with quality defensive gear and light weapons, are preferred by merchant concerns and government agencies operating in dangerous areas. A military spaceship is designed specifically for combat and is available only to the federal navy, the Astroguard services, and the transport branches of military ground forces.
Crew Required. The minimum number of crew members required to keep the spaceship running and trouble-free, excluding gunner for the ship's burster or any crew necessary to service any pods the ship possesses.
Passenger Capacity. The maximum number of people the spaceship may accommodate when no pods are attached. Accommodations are basic: shared sleeping quarters, galley, and first aid station (fulfils equipment requirement for diagnosis and treatment tasks, provides no Skill Level increase). Any crew required to run the ship takes up passenger space.
Cargo. The maximum metric tonnage of cargo that the spaceship can transport. Cargo space may be increased by 0.1 ton per passenger below passenger capacity carried. The cargo hold will not sustain life.
Cost. Price in Trans for the spaceship hull when new if purchased on a world of the same or higher Civ Level as the hull. Price may fluctuate as described in 18.0.
Performance Modifier (PM). A quantification of the ship's responsiveness and structural integrity. Applied to the chance to avoid an accident, in accordance with 11.2.
Base Repair Time. Spacecraft Engine, Bridge and Hulls have a Base Repair Time of 24 hours while Spacecraft Pods and Forcefields have a Base Repair Time of 12 hours.
Any hull designed should be given ratings and attributes comparable to those found on the Spaceship Attribute Chart (Delta Vee Table 4.9) and in 31.2. The spaceship may be made capable of carrying any number of pods. The Energy Burn Rate of a spaceship should be 20% to 50% greater than the number of pods it may carry. The cost of a spaceship hull is calculated by adding together the costs of all the following attributes:
If the spaceship is streamlined, increase all the preceding by 50%. These costs are based on the number of pods the ship is capable of carrying, not the number it is actually carrying at any particular time.
The concept of how pods work and details on combat abilities of certain pods can be found in Delta Vee 1.0 and 5.0, especially in Table 5.8 (the Pod Attribute Chart). The following pods are the types most commonly used on spaceships.
Each description includes the Pod's Availability, the Crew Required to operate the Pod, the Pod's Passenger Capacity and Cargo Capacity in Tons, the Civ Level at which the Pod initially becomes available and Cost in Trans. These attributes are similar to those in 31.2.
Unless a pod is assigned a specific Armor Class by the Pod Attribute Chart, it is considered to be Armor Class 0. At an additional cost of 50 Trans, a pod may be purchased at Armor Class 1. At an additional cost of 400 Trans, a pod may be purchased at Armor Class 2. Any crew required to run a pod without passenger capacity must be housed elsewhere on the spaceship.
A psionic navigator conducts and controls instantaneous interstellar travel, or hyperjumping, by manipulating magnetic monopoles with his mind. A hyperjump occurs when the thought patterns of a psionic mind concentrating on a remote destination are encoded into a plate of monopoles. The mental image and the power of the navigator's mind force the perpetually unidirectional particles to reverse their polarity, causing a shift or jump to the point matching the monopole pattern. This inexplicable phenomenon is the key to both humankind's galactic expansion and the psionic community's continued economic well being.
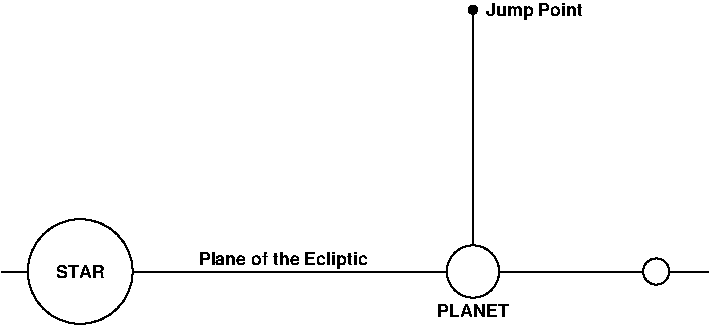
Failure of a navigator to wrest the monopoles to his mental command often results in a jump error and/or psychic damage to the psion. Gravitational fields increase this risk by disrupting the stability of the monopole screen that the navigator projects his mind onto. Because of this, spaceships must travel to the outskirts of a star system by conventional propulsion before a jump may be conducted. Conversely, the destination of a jump must be outside the gravity wells of the system so that the navigator's mind and the integrity of the ship will not be destroyed by monopoles reacting to forces other than his own thoughts. The point outside a star system that is closest to a given planet and yet far enough away from all gravitational fields in the system to conduct a safe hyperjump from is called that system's jump point. It is to this point that a navigator will bring a spaceship as the result of a perfect jump.
A standard jump pod, an augmented jump pod, a hunter pod, and an explorer pod each contains a jump engine. Any spaceship with one of these pods may hyperjump. Exception: The engine in a hunter or explorer pod may not be used when attached to a ship capable of carrying more than 3 pods. The Corco Omega lifeboat also contains a jump engine.
A jump engine does not consume energy; however, with the exception of the augmented jump pod, all hyperjump engines lose their stability after a time. A standard jump pod must be serviced as described in 31.4. The hunter pod, the explorer pod, and the Omega each contains a burn-out hyperjump engine. After a few jumps, such an engine must be entirely replaced. A hunter pod engine must be replaced after three jumps at a cost of 500 Trans. An explorer pod engine must be replaced after two jumps at a cost of 375 Trans. A Corco Omega engine must be replaced after one jump at a cost of 200 Trans.
A jump point for departing or arriving at a given planet lies above or below the plane of the ecliptic for the star system, such that a line drawn from the point to the planet would be perpendicular to the ecliptic.
See diagram below.

The length of this line depends on the Spectral Class of the planet's star and the distance between the planet and the star. Subtract the distance (in AUs) between the planet and the star from one of the following numbers:
| Spectral Class A: | 180 |
| F: | 130 |
| G: | 90 |
| K: | 60 |
| M: | 41 |
The result of this subtraction is the minimum distance (in AU) from the planet a spaceship must be to go into or come out of a jump. For example, the minimum jump point for a planet that is 7 AU from a Class K star is 53 AU. This distance would have to be traversed using normal propulsion and could take as long as four weeks (for an A Class star); see 33.0.
Note: A spaceship must be stationary (at 0 velocity) at the moment of hyperjump, and will thus be stationary when it comes out of hyperjump.
A hyperjump is conducted using the Hyperjump Table (32.3) in accordance with the navigation skill description (see 10.0).
See Table 32.3.
| percentile dice minus hyperjump chance |
psionic backlash check |
jump outcome and spacecraft location |
|---|---|---|
| −40 or less | No | Perfect Jump; perpendicular to the plane of the system ecliptic, directly above the destination planet at the closest safe jump point |
| −39 to −20 | −50 | Perfect Jump: Perpendicular to the plan of the system ecliptic, directly above the destination planet at the closest safe Jump Point |
| −19 to 0 | −40 | Perfect Jump: Perpendicular to the plan of the system ecliptic, directly above the destination planet at the closest safe Jump Point |
| +1 to +10 | −30 | Good Jump: Perpendicular to the plan of the system ecliptic, directly above the destination planet and 1 Die roll in AUs beyond closest jump point. |
| +11 to +20 | −20 | Good Jump: Perpendicular to the plan of the system ecliptic, directly above the destination planet and 2 Die rolls in AUs beyond closest jump point. |
| +21 to +30 | −10 | Slight Jump Error: Perpendicular to the plan of the system ecliptic, directly above the destination planet and a Percentile Die roll in AUs beyond closest jump point. |
| +31 to +40 | 0 | Minor Jump Error: Perpendicular to the plan of the system ecliptic, directly above the destination planet and 10x a Percentile Die roll in AUs beyond closest jump point. |
| +41 to +50 | +10 | Major Jump Error: A Perfect Jump to the star nearest the destination star with the same Spectral Class letter. |
| +51 to +60 | +20 | Major Jump Error: The GM uses one die to determine the random destination. The destination star is used as the zero point. |
| +61 to +70 | +30 | Jump Randomised: The GM uses two dice to determine the random destination. Sol is used as the zero point. |
| +71 to +80 | +40 | Jump Failure: The Hyperjump does not occur and the spacecraft's jump engine suffers Heavy Damage |
| +81 to +90 | +50 | Jump Randomised: The GM uses percentile dice to determine the random destination. Sol is used as the zero point. |
| +91 or more | +60 | Jump Disaster: Within the gravity wells of the destination star system. Use the Equipment Damage column of the Hit Table (30.9) to check for Spacecraft damage; roll two dice and add 15 to the dice result. |
Random Destination: The GM secretly rolls the indicated die or dice three times to determine three coordinates. The first roll determines the X coordinate; the second roll determines the Y coordinate; and the third roll determines the Z coordinate. If the result of a roll is an even number, the coordinate is positive; if the result is an odd number the coordinate is negative. The GM secretly locates the three coordinates results on the Interstellar Display and informs the character that they are lost in space. A character may attempt an Astronomy skill task to determine their location (see 12.0). It is possible that a random destination will lie off the Interstellar Display.
Commercial hyperjump voyages occur with a varying degree of regularity between many stars. The frequency and reliability of a commercial voyage between two stars depends on the distance between them and the highest Spaceport Class of a world orbiting each star. Commercial interstellar travel always begins and ends at the world in a star system with the highest Spaceport Class (by federal law). If two or more worlds in a system share the highest class, the GM chooses one as the interstellar terminal.
The Interstellar Route Chart is used to determine the type of route (if any) that exists between any two stars. The highest Spaceport Class in the destination star system is cross-referenced with the highest Spaceport Class in the system of departure to yield three numbers, each defining the maximum distance (in light years) at which a given type of route exists.
A green jump route is a well-travelled commercial lane with passenger and freight service occurring daily (or more often). If a character or party wishes to travel this route, roll percentile dice to determine how many hours he must wait for a ship with available space.
An Amber jump route is an infrequently travelled commercial lane traversed by freighters and an occasional passenger vessel. Roll two dice to determine how many days a character must wait for available space on this route.
A Red jump route is a rarely travelled course traversed by a few exploratory and resupply ships. Roll percentile dice to determine how many days a character must wait for available space on this route.
When using the Hyperjump Table for a spaceship that a character has booked passage on, assume the ship's navigator has a Skill Level of 7, a Mental Power Rating of 6, is in a standard jump pod, and either frequents or has previously visited both star systems at some time.
The price of standard passage on a commercial interstellar spaceship is calculated with the following formula:
(Distance in LY's × 100 Mils) + (Distance in AUs to and from each world's jump point × 20 Mils)
Standard passage includes a small room shared with two or three other passengers, a common toilet, a common dining area, and a baggage allowance of 100 kg. The price of a standard passage on a red jump is increased by 50%.
A character travelling a green jump (only) may book luxury passage at 2.5 times the standard fare. A luxury passenger receives a private room (single or double occupancy, as requested) with private bath, a common recreation-bar-dining area featuring entertainment and gourmet dining, and a baggage allowance of 500 kg.
The total time of an interstellar voyage equals the time to travel from the world of departure to its jump point, and from the destination world to its jump point, in accordance with 33.0. The actual hyperjump takes no time.
See Table 33.5.
| destination starport | ||||||
|---|---|---|---|---|---|---|
| ½ | 1 | 2 | 3 | 4 | 5 earth |
|
| ½ | None | None | 0/0/2 | 0/0/6 | 0/0/10 | 0/0/15 |
| 1 | None | 0/0/5 | 0/0/10 | 0/2/15 | 0/6/20 | 2/10/15 |
| 2 | 0/0/2 | 0/0/10 | 0/10/20 | 2/15/25 | 6/20/30 | 10/25/35 |
| 3 | 0/0/6 | 0/2/15 | 2/15/25 | 10/20/30 | 15/25/35 | 20/30/45 |
| 4 | 0/0/10 | 0/6/20 | 6/20/30 | 15/25/35 | 20/30/45 | 30/40/50 |
| 5 earth |
0/0/15 | 2/10/25 | 10/25/35 | 20/30/45 | 30/40/50 | — |
If the distance (in light years) is equal to or less than the first number, a green jump route exists. If the distance is greater than the first number but less than or equal to the second number, an amber jump route exists. If the distance is greater than the first and second numbers, but less than or equal to the third number, a red jump route exists.
See 32.4.
Travel between the worlds of a single star system, or between a world and its jump point is conducted at slower than light speeds (STL). The most common sub-light spaceship engine is a reaction drive, using radioactive elements as fuel.
In an interplanetary journey, a spaceship accelerates at a constant
rate to the journey's mid-point and then decelerates at the same rate
until it reaches its destination. Thus, the longer the journey, the
higher the velocity the ship will attain at its turn over
point.
All interplanetary distances are measured in AUs. The time required
for the journey depends on the spaceship's rate of acceleration. A
constant acceleration/deceleration of 1 G is the usual travel
speed for a spaceship. The travel time using this speed is calculated
with the following equation:
d = distance in AUs
A spaceship without special equipment manned by a healthy crew may travel at a constant acceleration/deceleration as high as 2.5 G. This speed equals an acceleration or deceleration of 1 per turn in Delta Vee. The travel time using this method is calculated with the following equation:
A high performance spaceship (Velocity Rating of 2 or 3) manned by a crew who all have internal gravity webs may travel at a constant acceleration/deceleration as high as 5 G. The speed is often used in long range military pursuit and equals an acceleration or deceleration of 2 per turn in Delta Vee. The travel time using this method is calculated with the following equation:
This distance may be as little as the difference between their distances from the star, or as great as the sum of their distances from the star (if the two planets are on exact opposite sides of the star). For example, the 11th and 12th planets on the Star System Log could be as close to each other as 15 AUs and as far apart as 65 AUs. Unless the GM wishes to determine the length of each planet's orbital year and set up an ever changing orbital model, he should use the following simplification to determine planetary distances: The distance between two worlds equals the distance from their star to the world of the two that is furthest from the star. Thus, the distance between the planets mentioned above would be 40 AUs.
For purposes of calculating interplanetary distances, a moon is considered to occupy the same position as its planet. The distance between a planet and any of its moons is left up to the GM. As a guideline, our moon is .0026 AUs (360,000 km) from the Earth. At a constant 1G acceleration/deceleration, a journey from the Earth to the moon would take about 3.5 hours.
An Energy Unit for a reaction drive engine consists of one kilogram of
radioactives and costs 300 Mils. Thus, it would cost
43 Trans to fill up
an energy pod capable of carrying 144
Energy Units. Energy is always available at a Class 3,
4, or 5 spaceport. Energy may be available at a
Class 1 or 2 spaceport; see
25.5. Any spaceport orbiting a world that
contains radioactives as a resource will always have spaceship energy.
As explained in Delta Vee , the number of Energy Units a spaceship expends to maneuver depends on its Energy Burn Rate, which corresponds to the number of Energy Units in one Energy Block for that ship. The same concept applies to long-range interplanetary travel. A spaceship that is travelling at a constant acceleration/deceleration of 1 G must expend 1 Energy Block every 24 hours (or fraction thereof). A ship that is travelling at 2.5 G must expend 1 Energy Block every 6 hours. A ship that is travelling at 5 G must expend 1 Energy Block every hour. A spaceship that is lifting off from the surface of a world must expend an additional number of Energy Blocks equal to the size of the world (1 to 9). Lift-off does not increase the voyage time.
The GM must make sure that any spaceship he enters into play possesses the requisite energy to complete any voyage planned for it. Sometimes two or three energy pods will be required for a large ship travelling to and from jump points.
A gravity web contains and protects a person's organs and arteries during the strain of high G acceleration and deceleration. The web is inserted throughout the person's body in a complex series of operations. All star sailors are provided with a gravity web, as are many members of the Astroguard. A character may undergo an operation for gravity web implantation on any world with a Civ Level of 7 or higher. The operation costs 15 Trans and the character will be in the hospital for 7 days.
A character without a gravity web cannot survive an extended period of acceleration or deceleration greater than 2.5 G. When playing Delta Vee, a character without a gravity web cannot survive a velocity change of more than 2 (5 G) in a single Command Phase.
The frequency of commercial voyages between two worlds depends on the class of their spaceports. The Interplanetary Route Chart is used to determine the type of route (if any) that exists between any two worlds in the same system. The Spaceport Class of the destination world is cross-referenced with the Spaceport Class of the world of departure to yield the type of route: course green, course amber, or course red. The frequency and quality of service on these routes correspond to those of the jump routes of the same color designations in 32.4.
The price of standard passage on a commercial interplanetary spaceship equals the distance of the voyage (in AUs) multiplied by 40 Mils. If the spaceship must lift off from the surface of a world (Spaceport Class ½) or if the voyage is course red, the fare is increased by 50%. In any case, the minimum cost for any interplanetary voyage is 250 Mils (including a voyage from a planet to one of its moons and vice versa).
A character travelling on a course green voyage of at least one AU may book luxury passage at 2.5 times the standard fare. He receives the comforts of luxury passage described in 32.4. A commercial vessel always travels at a constant acceleration/deceleration of 1 G.
See Table 33.5.
| destination spaceport | |||||
|---|---|---|---|---|---|
| ½ | 1 | 2 | 3 | 4 | |
| ½ | - | R | R | R | A |
| 1 | R | R | R | A | A |
| 2 | R | A | A | G | G |
| 3 | R | A | G | G | G |
| 4 | A | A | G | G | G |
R: Course Red. A: Course Amber. G: Course Green. (-): No Route. See 33.5 for details.
When the characters are in a spaceship that encounters another spaceship, combat may occur. If possible, the characters should avoid spaceship combat; it is deadly. However, situations will certainly arise where combat is inevitable. When this happens, the GM and the players use the Delta Vee tactical space combat system to resolve the battle. Delta Vee is complete unto itself and may be used as is, if the characters are in a ship that they are not controlling. The following rules modify the system, allowing characters to participate directly in the conduct of combat. Combat burns up energy at a much faster rate than steady, uninterrupted travel. Conserving enough energy during battle so that the ship may get somewhere if it survives should be as much on the characters' minds as victory.
Keeping in/mind that each hex on the map is 20,000 km across, the GM may arrange the maps in any configuration and may place planets, asteroids, the characters' spaceship, and any spaceships encountered on the maps to match the situation he is describing. Unless the spaceships are near a world or jump point that they are travelling to or from, they will be travelling much faster than the velocities in Delta Vee. In this case, the Velocity markers assigned show their velocities relative to each other. The slowest ship should be assigned a 0 Velocity marker, and the others should have markers indicating their velocities in comparison with the slowest ship. If the GM wishes, he may use markers of his own devising to show velocities above 9.
When in the bridge or certain pods of a spaceship, a character may use his space combat skills, as described in Delta Vee 9.2. At the beginning of any friendly Command Phase during space combat, a character may declare that he is moving to another part of the ship. If he does so, his skills may not be-used at all for that Command Phase and the next friendly Fire Phase. At the beginning of the following friendly Command Phase, the character may again use his skills (as allowed by his new location).
Unless the GM determines Skill Levels for the crew manning a spaceship that the characters encounter, he should use the Delta Vee system unmodified for their maneuvers, commands, and fires.
A character in a compartment that becomes vulnerable is not harmed. A character in a compartment that becomes damaged must use the Hit Table, as if struck with a Hit Strength of 6 (see 30.1). A character in a compartment that is destroyed must use the Hit Table, as if struck with a Hit Strength of 20. If he survives this injury, and he does not pass out, he may immediately move to any other compartment. If he passes out as a result of the injury he dies.
Spaceship armor in Delta Vee uses a different classification system than personal and vehicle armor in Universe. If a situation should arise where a spaceship's armor is hit by forces other than spaceship weaponry, the Armor Classes of each pod and compartment can be translated into projectile and beam Defence Ratings as follows: Armor Class 0: 2/2. Armor Class 1: 4/4. Armor Class 2: 6/6. A spaceship's force field may never be pierced by any projectile weapon.